Using GlyphMath ↩

Adapted from the original RoboFab documentation.

If they’re compatible, Glyph objects can be used in Python math expression: you can add, subtract, multiply and divide them like normal numbers or variables. The math is applied to the coordinates of each point in the glyph. The result of a GlyphMath operation is a new glyph. You can then insert this glyph in a font, or use it for other math operations.

operation	GlyphMath	description
addition		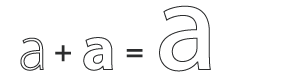The coordinates of each point are added.
subtraction		The coordinates of each point are subtracted. Note that although the glyph looks unrecognisable, all points are still there. Literally the difference between the two glyphs.
multiplication		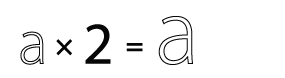Scaling the glyph up. When you multiply with a tuple like (1.3,1.05), the first value is used to multiply the x coordinates, the second value is used for the y coordinates.
division		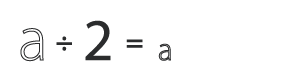Scaling the glyph down. When you divide with a tuple like (30,29), the first value is used to divide the x coordinates, the second value is used for the y coordinates.
various		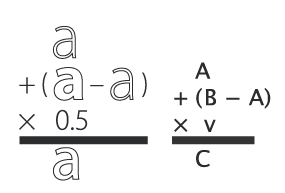Combination of operations to make a real interpolation.

You can use GlyphMath to create interpolation effects, transplant transformations from one glyph to another and superimpose several effects at once.

f = CurrentFont()

# two interpolatable, different glyphs
a = f["A"]
b = f["B"]

# multiply works as scaling up
d = a * 2
# or
d = 2 * a
f.insertGlyph(d, name="A.A_times_2")

# # division works as scaling down
d = a / 2
f.insertGlyph(d, name="A.A_divide_2")

# addition: add coordinates of each point
d = a + b
f.insertGlyph(d, name="A.A_plus_B")

# # subtraction: subtract coordinates of each point
d = a - b
f.insertGlyph(d, name="A.A_minus_B")

# combination: interpolation!
d = a + .5 * (b - a)
f.insertGlyph(d, name="A.A_interpolate_B")